Question

ما هي حسابات توازن الصنف؟

ما هي قاعدة الأطوار Phase Rule؟

أمثلة على قاعدة الأطوار؟

Answer 1

قاعدة الأطوار Phase Rule

 - اكتشفت معادلة الأطوار أول مرة من قبل العالم ويلارد كيبس في عام 1878 ونظراً لنشرها فى مجلة غير مشهور فقد بقيت هذة المعادلة قيد النسيان حوالي 20 سنة.

- إن هذه المعادلة تعطي العلاقات بين عدد درجات الحرية F) Degree of freedom) لنظام يحتوى على مجموعة متزنة من المكونات C) Components) مع عدد أطوار P) Phases) الموجودة فى النظام.

- تنص قاعدة الأطوار Phase rule على أن:

عدد درجات الحرية (F) وعدد الأطوار (P) وعدد المكونات (C) في نظام موجود في حالة إتزان تام ترتبط فيما بينها بالعلاقة الآتية:

F = C - P + 2

أولاً/ عدد درجات الحرية Degree of Freedom

- يوجد نوعين من الخصائص يمكن بواسطتها وصف الطور فى النظام (أى نظام) وأحدى هذه الخصائص تسمى بالخصائص الشاملة (Extensive Properties) وهذا النوع من الخصائص يعتمد على كمية الطور مثل وزن الطور وحجمه، أما النوع الثاني من الخصائص يسمى بالخصائص المكثفة أو المركزة (Intenstive properties) وهذا النوع من الخصائص لا يعتمد على كمية الطور وتكون قيمة الخاصية متساوية سواءاً للطور بكامله أو لأى جزء منه مثل الكثافة ودرجة الحرارة ومعامل الانكسار.

- الخصائص المكثفة أو المركزة هي التى تهمنا عند توضيح درجات الحرية حيث أن عدد درجات الحرية يعنى عدد المتغيرات المكثفة التى يمكنها اختيارها بصورة مستقلة لمي نتمكن بوساطتها تعريف النظام تعريفاً كاملاً ومن ثم تصبح قيم المتغيرات المكثفة الأخرى ثابتة.

- فمثلاً بإمكاننا تحديد حالة نظام يتكون من سائل الماء فقط عند قيم محددة لدرجة حرارة الماء وضغطه لأنه في درجة حرارة وضغط معينين سوف تكون لسائل الماء قيم ثابتة لخصائصه المركزة مثل الشد السطحي ومعامل الانكسار والكثافة أو بمعنى آخر أنه بالامكان وصف العينة وصفاً كاملاً عندما نحدد أية خاصيتين من الخواص المكثفة لسائل الماء.

- نستنتج من ذلك أن عدد درجات الحرية للنظام المتزن يعني أقل عدد من المتغيرات المكثفة التى يمكن تغييرها بصورة مستقلة دون أن يحصل تغير في عدد أطوار هذا النظام.

ثانياً/ عدد المكونات Number of Components

- يمكن تعريف عدد المكونات بأنه أقل عدد من المواد الكيميائية القابلة للتغير بصورة مستقلة والموجودة في أطوار النظام المختلفة.

- فمثلاً في نظام السائل وبخاره والذي يوجد فيه طوران هما الطور السائل والطور البخاري فأن هذا النظام يحتوى على مكون واحد بينما في حالة نظام المحلول الذي يحتوي على مذاب وبخار المذيب فإن النظام له طوران وكذلك مكونان وهنالك معادلة يمكن بواسطتها حساب عدد المكونات وهي:

C = N - R

حيث N : العدد الكلي للمواد الكيمياوية الموجودة فى النظام

R : تمثل عدد التوازنات الكيميائية والنسب المتكافئة بين بعض الاصناف التركيبية في النظام

- أما في حالة المحاليل الايونية فإن المعادلة السابقة ستحرر إلى الشكل الأتي:

1 - C = N - R

أمثلة لتحديد عدد المكونات

- إن عملية تحديد عدد المكونات يتطلب:

(1) معرفة عدد المركبات الكيميائية الموجودة فى النظام وهو فى حالة الإتزان.

(2) معرفة عدد المعادلات الكيميائية التى تربط بين هذه المكونات. 

(3) معرفة العلاقة بين تراكيز المكونات الكيميائية.

وإليك بعض الأمثلة توضيحية لتحديد عدد المكونات:

(1) عند إذابة ملح الطعام فى الماء تكون لدينا أربعة مركبات كيميائية وهي: ^-H₂O , NaCl , Na⁺ , Cl 

توجد هنالك حالة اتزان ما بين كمية NaCl المتفككة وكذلك عدد الأيونات المتكونة من ^-Na⁺ , Cl وهنالك توازن آخر وهو أن عدد أيونات +Na يجب أن يساوي دائماً عدد أيونات -Cl وبذلك فإن العدد الكلي للمكونات في هذا النظام يساوي:

C = 4 - 1 - 1 = 2

(2) عند خلط كميات من غازات لا تتفاعل مع بعضها البعض مثل الهيليوم والهيدروجين والأرجون ، فإن هذا الخليط يكون بحالة اتزان دائماً بغض النظر عن تركيز أى مكون من مكونات هذا النظام لذا فأن العدد للمكونات في النظام يساوي ثلاثة.

(3) عند خلط كمية من الغازات التى تتفاعل مع بعضها البعض مثل خلط كمية مع غاز الهيدروجين وغاز اليود وغاز يوديد الهيدروجين.

أن هذا النظام يحتوى على ثلاث مركبات كيميائية وهي H₂ , I₂ , HI ولكن هذه المركبات ترتبط فيما بينها بالمعادلة الكيميائية الآتية:

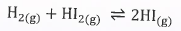
وهذا يعنى أن ثابت الإتزان K يساوي:

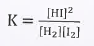
وكذلك فأن:

أى أن تركيز الغازين متساو وبذلك فإن العدد الكلي لمكونات مثل هذا النظام متساوي:

C = 3 - 1 - 1 = 1

(4) فى النظامين المتوازنين الآتيين:

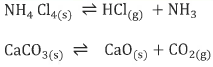
يعبر عن ثابت الإتزان للتفاعل الأول كالتالي:

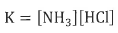
كم أن المكونين HCl , NH₃ متساويان فى التركيز:

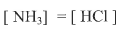
وبذلك فأن العدد الكلى للمكونات يساوي 

C = 3 - 1 - 1 = 1

أما ثابت الأتزان فى المعادلة التانية هو:

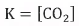
لا يمكن لهذا النظام أن يعامل مثل معاملة النظام الأول (نظام كلوريد الأمونيوم) لأنه بالرغم من أن عدد مولات CaO يساوي عدد مولات CO₂ ولكن تركيزهما غير متساو ، وبذلك فأن العدد الكلي لمكونات هذا النظام يساوي:

C = 3 - 1  = 2

Answer 2

ثالثاً/ عدد الأطوار Number of Phases

- الطور يمثل ذلك لجزء من النظام المتجانس فيزيائياً وكيميائياً في كل جزء من إجزائه وتفصله عن الأكوار الأخرى حدود واضحة ومتميزة سميت بحدود الطور Phase boundaries.

- مثلاً وجود قطعة من الثلج في قدح من الماء تكون معالم القطعة واضحة وكذلك حدودها التى تفصلها عن الماء وهي تمثل الطور الطلب الذي توجد لدية حدود تفصله عن الطور السائل.

- النظام المتجانس Homogenous system هو النظام الذي يتكون من طور واحد فقط أما النظام الذي يتكون من أكثر من نظام فيسمى نظام غير متجانس Heterogenous system.

أمثلة لتحديد عدد الأطوار

(1) الثلج يمثل طوراً واحداً إذا كان على شكل قطع صغيرة أو كبيرة ,لكن في حالة وجود عدد من الأشكال البلورية المختلفة من الثلج لا يمكن عدها طوراً واحداً ولكن كل شكل بلوري منها يمثل طوراً واحداً.

(2) وجود ملح الطعام فى الماء يمثل طوراً واحداًمتجانساً بالرغم من احتوائه على أيون الصوديوم وأيون الكلور فى الماء.

(3) وجود خليط من الغازات تامة الامتزاج تعد طوراً غازياً واحداً.

(4) خليط السوائل تامة الامتزاج يعد طوراً واحداً.

(5) خليط السوائل عديمة الامتزاج تكون أكثر من طور وعدد الأطوار فيها يساوي عدد الحدود الفاصلة بين الأطوار + 1

(6) المحاليل المتجانسة للمواد الصلبة المختلفة تكون طوراً واحداً بغض النظر عن المركبات الكيميائية التى تكونها.

(7) كل شكل بلوري خاص من المواد الصلبة ويشكل طوراً واحداً في حالة تشابه التركيب الكيمائي أو اختلافه، فمثلاً فمثلاً كل صورة بلورية من صور الكبريت تكون طوراً مستقلاً عن الشكل البلوري الآخر.