تحويل الصيغ ثلاثية الأبعاد إلى إسقاط فيشر
- عندما يكون لجزئ ما مركز كيرالي واحد فأن رسم إسقاط فيشر يكون أمراً سهلاً حيث يتم وضع المجموعة الأقل في الأولوية للأعلى ثم ترتب باقي المرتبطات في اتجاه عقارب الساعة أو عكس عقارب الساعة وذلك اعتماداً على توزيع المركز الكيرالي.
- ولكن عندما يحتوي الجزئ على أكثر من مركز كيرالي فأن تحويل الصيغة ثلاثية الأبعاد إلى إسقاط فيشر يصبح أكثر تعقيداً وكلما زاد عدد المراكز الكيرالية كلما زاد الأمر تعقيداً ولكن سوف نقتصر على الجزيئات التي تحتوي مركزين كيراليين فقط (بدون استخدام التوزيع الكيرالي).
- لتوضيح ذلك سنقوم باقتراح أربع هيئات مجسمة للمركزين الكيراليين والرابطة في مستوى الورقة وذلك من اليسار إلى اليمين.
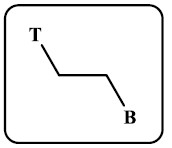
(1) الهيئة المجسمة BT
- في هذه الهيئة تكون المرتبطتين على كل مركز كيرالي اللتان تقعان في مستوى الورقة من اليسار إلى اليمين في وضعية Bottom-Top
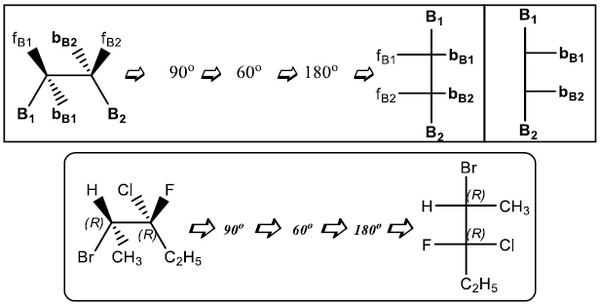
- سوف نرمز للمجموعة التي تقع خلف مستوى الورقة behind بالرمز b والتي تقع فوق مستوى الورقة front بالرمز f وبالتالي سيكون لدينا الرموز (bB , fB , bT , fT ) للمجموعات الأخرى.
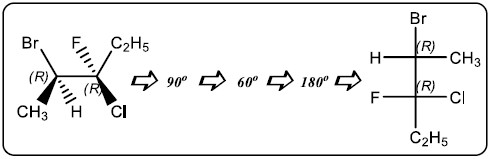
- لتحويل التركيب الثلاثي إلى إسقاط فيشر نقوم بتدوير الجزئ في اتجاه عقارب الساعة بزاوية 90o في مستوى الورقة ثم يتبعه دوران عمودي على نفس المستوى بزاوية o60
- وبعد ذلك نعمل التفاف للمركز الكيرالي الثاني فقط بزاوية 180o فتصبح رابطة الإسفين المتقطع bB على الجانب الأيمن في إسقاط فيشر وتكون رابطة الإسفين المتقطع bT على الجانب الأيسر.
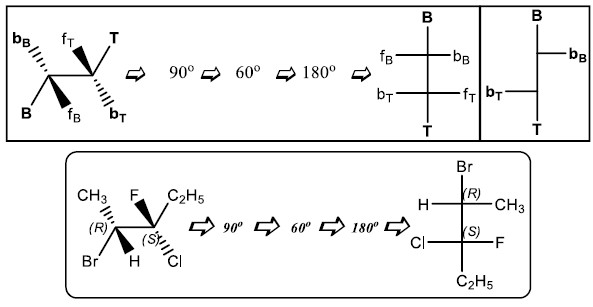
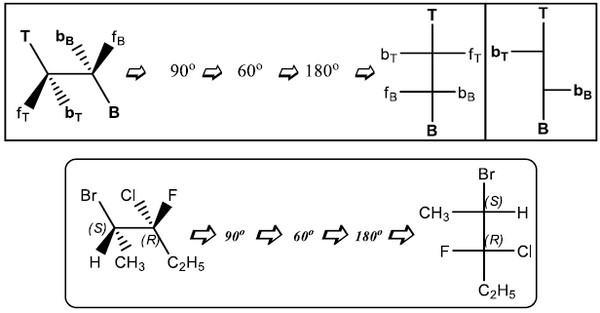
(2) الهيئة المجسمة TB
- وهي الوضعية التالية:
- عند تحويلها إلى إسقاط فيشر نقوم بنفس الخطوات السابقة فتكون رابطة الإسفين المعتم fT على الجانب الأيمن لإسقاط فيشر وتكون رابطة الإسفين المعتم fB على الجانب الأيسر وهي عكس الهيئة B.T
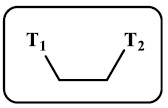
(3) الهيئة المجسمة TT
- في هذه الوضعية تكون المرتبطتين اللتان يقعان في مستوى الورقة للأعلى.
- وفي إسقاط فيشر تكون رابطتي الإسفين المتقطع على الجانب الأيسر.
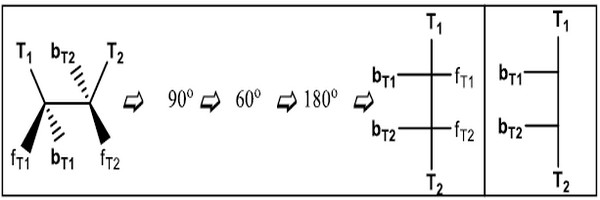
(4) الهيئة المجسمة BB
- في هذه الوضعية تكون المرتبطتين اللتان يقعان في مستوى الورقة للأسفل
- في إسقاط فيشر تصبح رابطتي الإسفين المتقطع على الجانب الأيمن وهي عكس الهيئة T.T