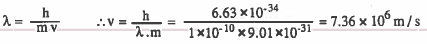الذرة والميكانيكا الموجية
نظرا لفشل نظرية بور في تفسير طيف الذرات عديدة الإلكترونات ، ونظراً لظهور تناقضات بين مباديء الكم التي افترضها العالم بور مع قوانين الميكانيكا . مما دعا الفيزيائيون إلى استخدام نظريات الميكانيكا الموجية لتفسير تركيب الذرة وهذه النظريات سميت بالنظرية الذرية الحديثة .
ومن العلماء اللذين ساهموا في ذلك وادخلوا نعديلات على نظرية بور:
(1) دي بروجلي (۲) هایزنبيرج (3) شرودنجر
أسس النظرية الذرية الحديثة
(1) الطبيعة المزدوجة للإلكترون للعالم دي بروجلي ( دي بروليه).
(2) مبدأ عدم التاكد للعالم هايزنبيرج.
(3) إيجاد معادلة مناسبة تصف الحركة الموجية للإلكترون، وتحدد اشكالها وطالتها للعالم شروسنجر.
الطبيعة المزدوجة للإلكترون للعالم دي بروجلية
- توصل آینشتاین Einsttein إلى أن الضوء عبارة عن سيل من الجسيمات مكونة من أجزاء صغيرة تسمى فوتونات وهذا يعني ان للضوء موجات تحمل بعض خواص الجسيمات.
- ومن ذلك وضع أينشتاين المعادلة التالية:
E = m . C2
حيث أن:
E= طاقة الشعاع بوحدة الجول (1)
m = كتلة الفوتون بوحدة الكيلو جرام (Kg).
C = سرعة الشعاع (3x 108 m/s)
- العالم بور افترض أن الإلكترون يدور حول النواة في مدارات محددة ، وأن طاقات إلكترون ذرة الهيدروجين ذات كميات محددة (مكممة) من الطاقة ، ولكن العالم بور لم يعطي تفسيراً لذلك حتى جاء العالم دي بروجلي واستطاع ان يفسر هذا اللغز.
- و اقترح دي بروجلي De Broglie عام 1924م أن تكون الأجسام ومن ضمنها الإلكترونات مثلها مثل الضوءلها طبيعة ثنائية (مزدوجة) أي تحمل خواص موجية وخواص الدقائق(أنها اجسام مادية ولها خواص موجية مثل الفوتونات) وقد استطاع العالم دي بروجلي من وضع معادلة لقياس طول موجة الإلكترون المتحرك:
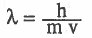
نص مبدأ دي بروجلي
"كل جسم متحرك يصاحبه حركة موجية لها بعض خصائص الموجات الصوتية ".
المشاهدات العملية التي تدل على أن للإلكترونات طبيعة موجية
(۱) عند مرور الإلكترونات خلال فتحة ضيقة او من خلال بلورات الفلزات فإنها تعاني حيودة وهذا الحيود يدل على وجود حركة موجية تصاحب الإلكترونات .
(۲) امكن تجميع الإلكترونات في بؤرة وانعكاسها فيها ، وهذه الملاحظة تتفق مع خواص الموجات الكهرومغناطيسية.
اشتقاق معادلة دي بروجلي
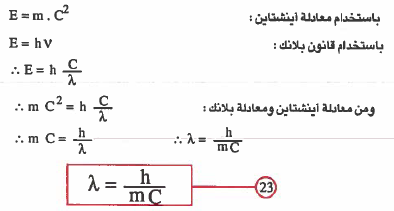
حيث أن :
λ = طول الموجة بوحدة المتر (m) .
h = ثابت بلانك وقيمته تساوي (3x 108 m/s)
C = سرعة الضوء (3x 10 m/s )
m = الكتلة بوحدة الكيلوجرام.
- وحسب مبدأ دي بروجلي فإنه نظرا لأن الإلكترونات تحمل صفات موجية فإنه يمكن تطبيق القانون السابق لإيجاد طول موجة الإلكترون مع فارق بسيط.
- والقانون هو:
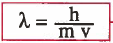
حيث أن :
λ: طول الموجة بوحدة المتر (m) .
v = سرعة الإلكترون .
m = كتلة الإلكترون بوحدة الكيلوجرام .
h = ثابت بلانك
ملاحظات هامة
(1) الفرق بين نظرية دي بروجلي ونظرية بلانك للضوء.
افترض بلانك أن للموجات الضوئية بعض خواص الدقائق الصغيرة أمادي بروجلي فقد اقترح أن الدقائق الصغيرة تحمل خواص موجية .
(2) نلاحظ الطبيعة الموجية في الأجسام الصغيرة كالإلكترون ولا نلحظها في الأجسام الكبيرة.
من معادلة دي بروجلي يتبين أن هناك تناسب عكسي بين كتلة الجسم المتحرك وطول موجته اي انه كلما زادت كتلة الجسم قل طول الموجة وبنلك لا | يمكن ملاحظتها (اكتشافها) (قياسها) ولذلك لا يمكن ملاحظة الطبيعة الموجية للكتل الكبيرة . أما الأجسام ذات الكتل الصغيرة مثل الإلكترونات فإن أطوال موجاتها كبيرة وبالتالي يمكن قياسها عملياً.
مسائل محلولة
مثال (1): أي من الأجسام التالية أطول موجة إذا كانت تسير بنفس السرعة : (1) إلكترون (2) جزيء (3) كرة قدم (4) حبة رمل.
الحل:
من القانون :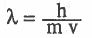 
يتبين أن هناك تناسب عكسي بين الكتلة وطول الموجة
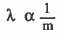
وهذا يعني أنه كلما زاد طول الموجة قلت كتلة الجسم. وحيث أن الإلكترون هو أقل الجسيمات في الكتلة إذن الإلكترون اطول موجة.
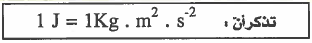
مثال (2): اوجد طول موجة بوحدة النانومتر لجسم سرعته (5x 105 m/s ) وكتلة الجسم 1500g ، وثابت بلانك = (6.63x 10-34 J.s)
الحل:
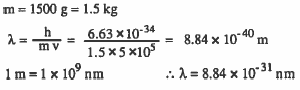
مثال (3): إلكترون طوله الموجي ( 1x10-10m) أوجد سرعة الإلكترون الذي كتلته (9.01x 10-31 kg) وثابت بلانك = (6.63x 10-34 J.s)
الحل :
