الأنحراف المعياري Standard deviation
- هو الجذر التربيعي الموجب لمتوسط مربعات إنحرافات القيم عن وسطها الحسابي.
- يرمز لها بالرمز (σ) وتنطق سيجما وأحياناً يرمز لها بالرمز (S)
- الانحراف المعياري هو أفضل المقاييس التي تُستخدم لقياس مدى تَفرُّق أو تناغم البيانات عن متوسطها الحسابي؛ حيثُ يُحسَب الانحرف المعياري من خلال إدخال جميع القيم وحسابها وليس من خلال قيمتين أو ثلاثة فقط، ومن هُنا تكمن دقّته عن باقي مقاييس التشتت.
- العلاقة الرياضية للانحراف المعياري:

- الوسط الحسابي = مجموع القيم / عددهم
مثال: أوجد الوسط الحسابي والإنحراف المعياري للقيم 5 , 6 , 7 , 8 , 9
الحل:
أولاً: حساب الوسط الحسابي
- الوسط الحسابي = مجموع القيم / عددهم
- الوسط الحسابي = (8 + 9 +7 + 6 + 5) / 5 = 35 / 5 = 7
أولاُ: حساب الإنحراف المعياري
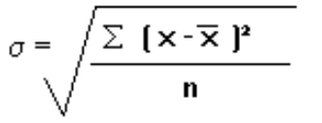
- نرسم الجدول التالي :

- بالتعويض فى القانون السابق نجد أن:
(10/5) √ = σ
1.41 = 2√ = σ
أمثلة أخري

الأنحراف المعياري النسبي Relative Standard Deviation
- يرمز له بالرمز RSD
- ويسمى أيضاً معامل الأختلاف (The coefficient of variation (CV ولكن الانحراف المعياري النسبي دائماً قيمة موجبة ولكن معامل الأختلاف قد يكون قيمة موجبة أو سالبة.
- قانون الانحراف المعياري النسبى أو معامل الأختلاف:
= (الأنحراف المعياري / الوسط الحسابي) * 100%
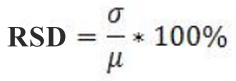
- وبتطبيق القانون على المثال السابق:
الانحراف المعياري = 1.41 ، الوسط الحسابي = 7 وبالتعريض فى القانون:
الأنحراف المعياري النسبي = (7 / 1.41) * 100% = 20.14%
الانحراف المتوسط Standard deviation of mean
- الانحراف المتوسط : هو أحد مقاييس التشتت وهو مجموع انحراف القيم عن المتوسط الحسابي مقسم على عدد القيم .
- الانحراف المتوسط = مجموع أنحراف القيم عن المتوسط الحسابي / عدد القيم
مثال: احسب الانحراف المتوسط للقيم 17 , 3 , 10 ؟
الحل:
- المتوسط الحسابي = (17 + 3 + 10) / 3 = 30 / 3 = 10
- مجموع انحراف القيم عن المتوسط الحسابي =
l (17-10) l + l (3 -10) l + l (10-10) l
7 + 7 + 0 = 14
عدد القيم = 3
الانحراف المتوسط = 14/3 = 4.66
أسباب استخدام المصطلحات السابقة.
- التشتت هو إحدى أهم خصائص البيانات التي تعمل على تحديد مقدار تناغم وتجانس القيم مع بعضها البعض، أو مدى تباعدها وتبعثرها عن بعضها البعض.
- فإذا كانت البيانات مُتتاغِمَة ومتقاربة من بعضها البعض حول نقطة معينة، فهذا يعني أنّها غير مُشتّتة بل متجانسة، أما إذا كانت البيانات متفرقة ومتباعدة عن بعضها البعض بحيث أنها لا تتجمع ضمن نقطة تركيز معينة، فهذا يعني أن هذه البيانات متشتتة.
- أما بالنسبة لمقدار التشتت يكون كبيراً إذا كانت البيانات متفرقة بشكل كبير، أما إذا كانت بُعد البيانات عن بعضها البعض قليل ومحدود، فهذا يعني أن مقدار التشتت قليل، وبمعنى آخر كلما زاد بُعد البيانات عن بعضها البعض زاد التشتت وكلما قلَّ بعد البيانات عن بعضها البعض قلَّ التشتت.
- وبما أنّ التشتت إحدى خصائص البيانات، فلا بد من وجود مجموعة من المقاييس التي تعمل على قياس مدى تشتت القيم أو تجانسها، من أشهر مقاييس التشتت المُستحدمة في علم الإحصاء:
المدى - نصف المدى الربيعي - الانحراف المعياري - الانحراف المعياري المتوسط - التباين.